Bahas Soal Matematika   »   Matriks   ›  

Jika matriks \( A = \begin{bmatrix} \ 1 & -2 \ \\[8pt] \ 0 & \ \ 1 \ \end{bmatrix}\), maka \(A^{25} \begin{bmatrix} \ 25 \ \\[8pt] \ 1 \ \end{bmatrix} = \cdots \)

1. \( \begin{bmatrix} -25 \\[8pt] 1 \end{bmatrix} \)
2. \( \begin{bmatrix} 25 \\[8pt] 1 \end{bmatrix} \)
3. \( \begin{bmatrix} -25 \\[8pt] -1 \end{bmatrix} \)
4. \( \begin{bmatrix} 1 \\[8pt] 25 \end{bmatrix} \)
5. \( \begin{bmatrix} 1 \\[8pt] -25 \end{bmatrix} \)

Pembahasan:

Untuk menyelesaikan soal ini, kita perlu mencari matriks dari \(A^{25}\) terlebih dahulu. Untuk cara cepatnya yaitu kita hitung dulu matriks \(A\) ketika dipangkatkan dengan angka yang kecil misalnya 2, 3, dan 4. Kemudian dari hasil yang diperoleh kita cari polanya. Setelah polanya ketemu kita dapat mencari matriks \(A^{25}\) dengan mudah.

Kita langsung aja hitung matriks \(A\) pangkat 2 dan \(A\) pangkat 3 sebagai berikut:

Dari hasil di atas, kita peroleh:

Jika persamaan umum untuk matriks \(A, \ A^2\), dan \(A^3\) di atas adalah \( \begin{bmatrix} \ a_{11} & a_{12} \ \\[8pt] \ a_{21} & \ a_{22} \ \end{bmatrix} \), maka kita peroleh pola untuk matriks \(A^n = \begin{bmatrix} \ a_{11} & U_n \ \\[8pt] \ a_{21} & \ a_{22} \ \end{bmatrix} \) di mana \(U_n\) adalah barisan aritmatika dengan suku pertama (a) dan bedanya (b) adalah -2. Kita peroleh \(U_n\), yaitu:

Jadi, matriks \(A^{25}\) yaitu:

Dengan demikian,

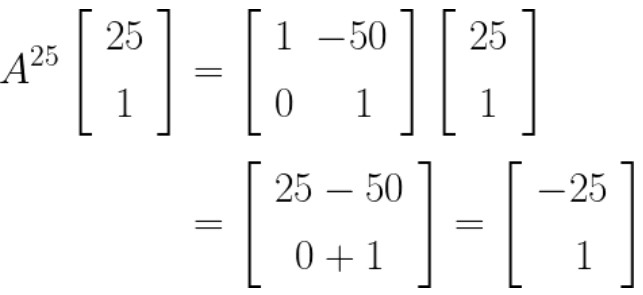
Jawaban A.